II.c.2) Relation espace-temps et vitesse
Le concept d’espace-temps ou continuum espace-temps apparait en inversant la définition de la vitesse. La vitesse n’est plus alors la relation entre l’espace et le temps et, par conséquent, l’espace et le temps commencent à dépendre l’un de l’autre pour que la vitesse de la lumière reste bien constante. Ce concept interdépendant configure la nature de l’espace-temps de la Théorie de la Relativité d’Einstein.
Mais expliquons-nous calmement…
Relativité du temps
La loi de la relativité du temps ressort de l’interprétation de l’expérience de Michelson-Morley, si deux espaces différents sont parcourus simultanément à la même vitesse, la seule manière de ne pas complètement se perdre consiste à rendre le temps relatif, effet connu sous le nom de dilatation du temps.
Dans la Théorie de la Relativité, le temps t0 mesuré par un observateur une horloge au reste au cours d’évènements se déroulant au même endroit reçoit le nom de temps propre de l’intervalle entre évènements.
Un exemple typique trouvé dans les livres pour expliquer le concept d’espace-temps et la dilatation du temps, se résume à un exemple d’horloge optique embarquée dans une navette spatiale et une autre fixe, sur Terre. Plus bas, nous détaillerons l’expérience mentale sur le concept d’espace-temps.
Depuis la Terre, un observateur verrait que le rayon de lumière de l’horloge optique zigzague solidairement à la navette alors que l’horloge terrestre va directement de haut en bas.
Par conséquent, vue la différence de distance parcourue par la lumière et la constance de sa vitesse, nous devons en conclure que le temps est différent pour chacun des observateurs. Cette différence ou dilation du temps, nous pouvons facilement la calculer :
t = t0 * (1 - v²/c²)-½
Evidemment, l’expérience mentale sur la structure de l’espace-temps est généralisable à l’ensemble des horloges et montres communes et la dilatation du temps est superbement testée par le mental : « …cette réponse est confirmée par des calculs détaillés sur ce qu’il arrive aux montres communes, vu depuis la Terre. »
Le concept de relativité du temps comporte plusieurs implications. Le concept de simultanéité en est un exemple important, il est également relatif et même le principe de conservation de l’énergie doit être reformulé pour maintenir sa validité. Dans le livre sur les Expériences de Physique, plusieurs expériences scientifiques sont proposées sur la mesure du temps et en particuliers, l’expérience du Train de la Grandsormière sur le problème de la simultanéité.
En ce qui concerne les voyages dans le temps, la dilatation du temps n’est pas à l’affut derrière chaque observateur, bien que certains scientifiques quantique-relativistes cherchent à obtenir au contraire.
Le paradoxe des jumeaux (horloges optique, normales ou personnes) complique la philosophie de l’espace-temps avec le problème de savoir lequel des deux observateurs sera dans le vrai car l’effet de la dilatation du temps de l’observateur terrestre sur l’horloge spatiale serait complètement symétrique pour l’observateur de l’horloge de la navette spatiale ou de l’horloge sur Terre.
La solution imaginaire du paradoxe des jumeaux nous arrive tout droit de l’application de la Relativité Générale. La mécanique relativiste nous dit que les systèmes de référence accélérés sont non-inertiels et il faudrait tenir compte des multiples accélérations et décélérations de la navette spatiale et des changements de systèmes de référence inertiels induits par ces changements de vitesse successifs.
Dans ce même livre, il existe une page dédiée au Paradoxe des jumeaux, où il est expliqué qu’il ne possède pas de solution et qu’il ne pourra pas en trouver au sein de la physique relativiste.
Les équations de transformations de Lorentz constituent une autre manière très compliquée de déduire la supposée nature relativiste de l’espace-temps ou relativité du temps. Elles étaient considérées comme un jeu mathématique jusqu’à ce qu’Albert Einstein découvrit leur véritable sens.
Les transformations de Galilée doivent être substituées par les équations de Lorentz afin que soit réalisés les deux postulats de la Relativité Restreinte : l’expression des lois physiques ne sera pas altérée et la vitesse de la lumière sera la même pour tous les observateurs.
Relativité de l’espace
La référence des mesures de l’espace peut être relative par rapport à l’observateur lui-même ou à un point extérieur à ce dernier mais il n’existe pas d’origine universelle de l’espace, ou bien elle n’est pas connue.
Le principe « tout mouvement est relatif » apparait encore ici, mais la relation entre l’espace et le temps relativiste ne se réfère pas à celui-ci, mais à l’effet de contraction de l’espace en fonction du système de référence dans lequel la vitesse est mesurée.
En d’autres termes, un mètre n’implique pas toujours le même espace, il dépend de l’observateur et de sa vitesse relative, la seule chose qui reste constante avec la philosophie de la courbure de l’espace et du temps, c’est la vitesse de la lumière ou relation espace-temps.
Ce concept de relativité de l’espace est déduit de l’expérience mentale de l’horloge optique alors que le rayon de lumière se déplace en direction de la navette spatiale et, bien sûr, de l’interprétation orthodoxe de l’expérience de Michelson-Morley.
L’hypothèse de la contraction des objets en mouvement est appelée contraction de Fitzgerald-Lorentz, elle est similaire et complémentaire de celle du temps, elle dépend de l’axe espace-temps qui est considéré comme affecté par le mouvement relatif entre les systèmes de référence, celui du temps et celui de l’espace.
Si l’on considérait seulement l’altération de l’espace, on aurait :
L0 = x'2 - x'1
L = L0 / γOù la relation de la transformation continue de dépendre de γ, concrètement de son inverse. Dans le cas où les deux axes sont affectés, seules les formules mathématiques seraient compliquées, car les raisonnements seraient les mêmes.
Dans le livre Physique et Dynamique Globale, l’analyse de mouvement de la lumière est approfondie dans la nouvelle théorie du tout. La Physique Globale assume une philosophie du temps et de l’espace de nature absolue.
Voyons maintenant une explication détaillée de l’expérience-exemple mentale de l’horloge optique de la Théorie de la Relativité.
Dans ce cas, la description de la réalité physique est, à mon avis, erronée car elle incorpore implicitement l’inertie de la lumière. Ce qui attire mon attention car ce concept de systèmes inertiels ou non-inertiels est précisément très utilisé dans ce domaine.
Un autre aspect très intrigant et certainement un peu effrayant concerne l’utilisation de l’expérience mentale, justifiée j’imagine par l’inexistence d’expériences physiques plus appropriées. Je dirais aussi que la réalité n’est pas celle qui est décrite dans l’expérience mentale suivante :
Hypothèses irréelles ou contradictoires
« Dans une navette spatiale, on tirera un rayon de lumière dans une direction perpendiculaire à cette de la navette, le rayon frappera un miroir et reviendra vers son point de départ. Un observateur de la navette verra les chemins aller et retour perpendiculaires au déplacement de la navette. Au contraire, comme la navette se déplace très vite, un observateur terrestre verra le mouvement de la lumière en zigzag, c’est-à-dire que selon lui, la distance parcourue sera supérieure à celle estimée par l’observateur de la navette »
Je considère que la vitesse de la lumière est additive à celle du champ de gravité de la Terre, mais pas celle d’un train. Dans l'espace ira de la même manière au sujet de son champ de gravité –l'Ether LUM (luminifère, universel et mobile)–, mais pas par rapport à la navette spatiale.
Le reste ne présente pas de difficulté, si on admet la constance de la vitesse de la lumière et que l’on suppose en plus l’inertie vectorielle de sa trajectoire et son trajet de retour, la distance parcourue par la lumière sera plus élevée. Ensuite, la seule solution possible est de rendre le temps relatif et d’inventer la nature relativiste de l’espace-temps.
Ici, nous nous trouvons de nouveau avec un triangle rectangle, le temps se serait dilaté suffisamment pour qu’avec une vitesse constante, le côté correspondant à l’espace initial (a)soit égal à l’hypoténuse (c). Cela signifie que le ratio de la dilatation temporelle sera l’inverse du cosinus de l’angle formé par ces deux côtés, ou ce qui revient au même que (c /a) qui coïncide avec la première variable auxiliaire des équations de Lorentz ; ou encore égal à l’inverse de la racine carrée de (1 - b²/c²), déduit du théorème de Pythagore où l’on coïncide en plus avec la seconde variable auxiliaire des transformations de Lorentz.
Expérience mentale (Fausse) 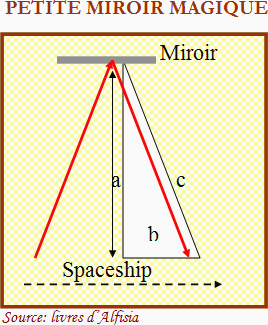
En vérité, cela me donne envie de demander : « Oh miroir, mon beau petit miroir magique, dis-moi quelle est la théorie la plus belle ? »
En plus, je crains bien que si nous avions plus d’observateurs ou de miroirs, nous obtiendrions plus de triangles avec un côté commun et nous nous verrions dans l’obligation de relativiser le relatif. Imaginez-vous la courbure de l’espace-temps que l’on pourrait obtenir avec deux grands hexagones.
D’autres exemples vus dans les livres de relativité, comme traverser une rivière avec une barque et prendre en compte le mouvement du courant sont similaires à celui que nous venons d’exposer sur la navette spatiale et la structure de l’espace et du temps.
