Perielio dell’orbita del pianeta Mercurio

4.b.3. Relatività d’Einstein e l’orbita del pianeta Mercurio

Se la predizione della Teoria della Relatività Generale di Einstein sulla curvatura della luce è più vistosa e spettacolare per come venne verificata con l’osservazione dell’eclisse del 1919, la spiegazione della precessione del perielio di Mercurio –deviazione rispetto alla Meccanica Celeste di Newton– è la più effettiva per il suo aspetto quantitativo.

Tuttavia, va notato che nel 1898 Paul Gerber spiegato che precessione prima fisica relativistica con esattamente la stessa formula.

Gli astronomi avevano osservato una deviazione rispetto alla Meccanica Celeste di Newton non spiegata da nessun fattore noto di 43,1'' di arco in 100 anni sull’asse dell’orbita del pianeta Mercurio, questa deviazione dell’orbita è ciò a cui mi riferirò come precessione del perielio di Mercurio, precessione dell’orbita di Mercurio o precessione di Mercurio, nonostante in senso stretto la precessione totale o somma della precessione spiegata e quella non spiegata sia abbastanza superiore. Se si calcola in gradi all’anno la precessione non spiegata, risulta in numeri tondi un diecimillesimo di grado all’anno.

Mediante le equazioni di campo tremendamente complesse della Meccanica Relativista, Einstein giunse ad una cifra molto vicina ai 43'' secondi di arco di precessione della suddetta orbita di Mercurio. –Vedi la pagina di mathpages* sulla spiegazione della Relatività Generale della precessione anomala dell’orbita di Mercurio.

Non c’è da stupirsi che di fronte all’adeguamento delle orbite dei pianeti ottenuto dalla Teoria della Relatività Generale si finisse accettando la relatività nel suo insieme, a scapito di altre alternative meno azzardate. Indubbiamente le equazioni della Relatività Generale di Einstein contengono alcune regole valide di comportamento della natura anche se mascherate nei loro meccanismi d’azione e di calcolo, come le idee di Paul Gerber.

Legge della Gravità Globale

Vediamo adesso se le Leggi di Gravità Globale spiegano anche la precessione del perielio di Mercurio.

L’espressione dell’accelerazione della gravità della formula apportata dalla Legge di Gravità Globale ci dà direttamente i risultati cercati sulla deviazione angolare e la componente normale dell’accelerazione o accelerazione centripeta.

Per conoscere la deviazione angolare totale in un giro o orbita di Mercurio l’unica cosa che dobbiamo fare è sostituire le variabili con i loro valori, prendendo in considerazione che g_g dovrà rappresentare l’accelerazione centripeta dovuta sia alla forza di gravità corrispondente alla legge di Newton che all’effetto Merlin o seconda componente dell’atractis causa aggiunta dalle Leggi di Gravità Globale.

Vale a dire, g_g sarà la componente normale dell’accelerazione o accelerazione centripeta che provocherà un giro completo all’orbita del pianeta più la precessione osservata per il periodo T.

Questo periodo T, per definizione del suo valore in trigonometria, causerebbe esattamente un giro completo se si considerasse esclusivamente la Legge di Gravitazione Universale di Newton dal momento che sappiamo che un’ellittica perfetta sarebbe conseguenza della legge dell’inverso del quadrato del raggio; come si osserva nelle leggi di Keplero dedotte dalle orbite dei pianeti della Meccanica Celeste.

La via rapida per calcolare la componente normale di accelerazione me la mostrò Sir Magufo in una piccola operazione pratica di matematica intuitiva. Ma prima di andare avanti riporterò i dati necessari per effettuare i calcoli, più il superfluo v, che sono:

G = costante di gravitazione universale = 6,67266 * 10^-11 (m² N / kg²)
c = velocità della luce = 2,99792458 * 10⁸ (m/s)
M = Massa del Sole = 1,98892 * 10³⁰ (Kg.)
r = raggio medio di orbita di Mercurio = 57,9 * 10⁶ (m)
T = periodo orbita di Mercurio = 7,60018 * 10⁶ secondi = 414,9378 orbite in 100 anni.
v = velocità media di Mercurio = 47948,31 (m/s)

Per la verifica empirica della formula della dinamica del pianeta Mercurio come parte della Meccanica Celeste di tutti i pianeti ed astri, sono stati eseguiti i seguenti passi:

• Semplificazione del caso dell’orbita planetaria circolare.

  È stato considerato il caso di un’orbita circolare del pianeta per semplificare i calcoli, perché il gioco di forze della gravità esisterebbe ancora e l’eccentricità dell’orbita del pianeta Mercurio è piuttosto bassa. Chiaramente è sufficiente per ciò che mi sono proposto.

• Calcolo dei giri per periodo con la Legge di Gravità di Newton.

  La formula della Legge di Gravità Globale si può scrivere con le sue due componenti:

  

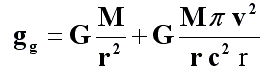
  In cui il primo termine della parte destra è la gravità della legge di Newton o accelerazione centripeta. La variazione angolare prodotta dalla stessa in un periodo dovrebbe essere, in teoria, uguale a un giro o 2π radianti. Dunque, se lo moltiplichiamo e lo dividiamo per v² e sostituiamo v²/r con la componente normale dell’accelerazione o accelerazione centripeta *a_n* otterremo:

  

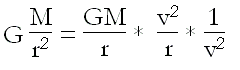
  E ricordando che il valore della velocità orbitale è la radice quadrata di GM/r otteniamo:

  

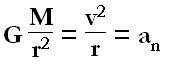
  v T = 2πr

  w T = 2π

  v / r = w

  a_n / v = w

  a_n T / v = T (v²/r) (1/v)

  = Tv/r = wT =

  = 2π Radianti Q.E.D.

  Siccome la componente normale dell’accelerazione a_n è legata al cambio della direzione della velocità con il tempo, se calcoliamo questo cambio per ogni m/s (dividendola per v) e la moltiplichiamo per il periodo T o numero di secondi totali in un giro ci darà per trigonometria 2π radianti o un giro intero dell’orbita del pianeta Mercurio o qualsiasi altro pianeta o astro della Meccanica Celeste.

  Quanto precede si può comprovare effettuando i calcoli utilizzando il valore della velocità media del pianeta Mercurio. –Un giro intero ha 2π radianti o 360º gradi, ogni grado ha 60' minuti ed ogni minuto 60'' secondi di arco.

  G			6,67266E-11
  Massa del Sole	1,98892E+30	GM	1,32714E+20
  Raggio medio orbita	5,79000E+10	an= GM/r²	3,95876E-02
  v media Mercurio	4,794831E+4	an / v = w	8,25631E-07
  Giri 100 anni	4,149378E+02
  Periodo T dell'orbita	7,60018E+06	w * T = 2 π	6,27494E+00

   

• Calcolo dei giri per periodo dovuti all’effetto Merlin.

  Ciò che davvero ci interessa è il secondo componente della formula della Legge di Gravità Globale, dato che sarà l’accelerazione centripeta provocata dall’effetto Merlin –derivata dalla doppia attrazione dovuta all’energia cinetica. Quest’accelerazione centripeta causerà la precessione del perielio di Mercurio (ppm), o dell’orbita di qualsiasi pianeta nella Meccanica Celeste, se la calcoliamo per tutto il periodo considerato come abbiamo fatto prima con a(n) per calcolare i 2π radianti.

  Secondo Sir Magufo si può risolvere direttamente l’integrale intuitiva dell’equazione differenziale non impostata se, dopo aver sostituito v²/r con a_n, poniamo il suo valore per un periodo intero, che, come abbiamo appena discusso, in termini di trigonometria sarà 2π

  L’integrale formale rispetto al periodo di tempo dell’accelerazione centripeta si risolve senza problemi, infatti, sia la velocità che l’accelerazione centripeta ed il resto delle variabili sono costanti o indipendenti dal tempo per la semplificazione a un’orbita circolare del pianeta Mercurio. Per questo, coincide con i calcoli basici di trigonometria perché l’integrale di *dt* è 1.

  Resterà quindi:

  

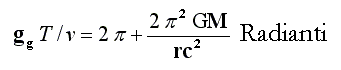
  Dunque, la precessione del perielio di Mercurio in radianti sarà:

  

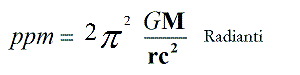
  Il valore della ppm ottenuto con l’uguaglianza precedente, derivata dalla Fisica Globale è 43,08'' secondi di arco ogni 100 anni come si mostra nella tabella seguente:

  G			6,67266E-11
  Massa del Sole	1,98892E+30	GM	1,32714E+20
  Raggio medio orbita	5,79000E+10	an= GM/r	2,29212E+09
  c²	8,98755E+16	GM / r c²	2,55033E-08
  π	3,141592654	π GM / r c²	8,01210E-08
  2 π Radiati/Giro	6,283185307	ppm = 2π² GM / r c²	5,03415E-07
  Giri/100 anni	4,14938E+02	radianti/100 anni	2,08886E-04
  Secondi/radiante	2,06265E+05	sec. arco/100 anni	4,30858E+01

  * * *

Ricordiamo che se in questa formula cambiassimo 2π con 6 ci darebbe la formula ottenuta da Paul Gerber 1898 e da Einstein nella Relatività Generale indipendentemente dall’eccentricità, come si menziona nel libro della Teoria della Relatività, Elementi e Critica.

Per la Terra la Relatività Generale dà un valore di 3,8 secondi di arco, la Fisica Globale di 4,02 ed il valore osservato è di 5 secondi di arco secondo la pagina di internet di Mathpages già citata.

Sebbene non vi siano dubbi che entrambe le teorie siano due approcci o due modi –tre se includiamo Paul Gerber– di vedere la stessa cosa in rapporto all’orbita del pianeta Mercurio, bisogna sottolineare che entrambe sono incompatibili fra di loro, perché si spiegherebbe due volte la stessa deviazione angolare.

 

Raggio medio 106 km	Pianeti	Radianti	Giri 100 anni	Totali radianti	Precessione secondo arco
					Valore osservato	RG	FG
57,90	Mercurio	5,03415E-07	414,93780	2,08886E-04	43.10	42,9195	43,08581
108,20	Venere	2,69387E-07	162,60160	4,38028E-05	8.65	8,6186	9,03498
149,60	Terra	1,94838E-07	100,00000	1,94838E-05	3,85	3,8345	4,01882
227,90	Marte	1,27897E-07	53,19150	6,80303E-06	1,36	1,3502	1,40323
778,30	Giove	3,74505E-08	8,43170	3,15771E-07		0,0623	0,06513
1427,00	Saturno	2,04259E-08	3,39440	6,93336E-08		0,0137	0,01430
2869,60	Urano	1,01574E-08	1,19030	1,20904E-08		0,0024	0,00249
4496,60	Nettuno	6,48217E-09	0,60680	3,93338E-09		0,0008	0,00081
5900,00	Plutone	4,94029E-09	0,40320	1,99193E-09		0,0004	0,00041

Si basano inoltre su principi diversi e contradditori; ciò che ci costringerà a ricorrere al rasoio di Occam, perché già esistono altri fenomeni naturali o esperimenti di fisica che aiuteranno a inclinare la bilancia in modo definitivo.

Con le Leggi della Gravità Globale, abbiamo verificato che si spiega esattamente la precessione del perielio di Mercurio, come conseguenza dell’effetto Merlin nell’interazione dell’Etere Globale (gravitazionale - cinetico - massa) con i corpi con massa.

In altri termini, il principio di uguaglianza tra massa gravitazionale e massa inerziale stabilito da Newton e mantenuto da Einstein è vago e inutile, perché il comportamento della massa fisica nella sua interazione con l’Etere Globale è lo stesso sia se si studia con o senza il campo gravitazionale; anche le forze agenti sono differenti.

Nella sezione sul Secondo Principio di Newton o Legge della Forza del libro della Fisica et Dinamica Globale vengono dettagliate le differenze fra la concezione di Newton, di Einstein e della stessa Fisica Globale, dovute a cambi intrinseci nella massa e nelle forze agenti.

Altri esperimenti concernenti alla orbite planetarie si trovano sulla pagine del Gravity Probe-B di questo libro e il Paradosso di Ultimo Delfino  di libro Astrofisica e Cosmologia Globale.

Vorrei infine sottolineare che non è mai stata abbandonata la geometria non curvata dello spazio euclideo, nonostante l’orbita del pianeta Mercurio, e Fisica Globale sostenuta da un modello fisico consistente con un tempo assoluto.

 

 

♦

Quando Einsaltro finì la pagina web,
andò tutto contento a dirlo a Principote e lui gli disse:

–Molto bene. E poi cosa hai fatto?–

Einsaltro, un po’ nel dubbio, gli disse:

–Mi sono messo a giocare a biglie
e a pensare al numero π.
Allora è apparsa una ragazzina pichetta,
si è buttata ai miei piedi,
e ha aperto le pigam…
fissando le mie pipallinine.–

E Principote rispose:

–Che pipacchiano!–