II.c.2.a) Teorema di Pitagora e la Relatività di Einstein
La Teoria della Relatività Speciale è legata a una gran complessità matematica, ma credo che la complessità sia molto più concettuale che matematica, poiché consiste essenzialmente nell’applicazione del teorema di Pitagora.
-
Non bisogna dimenticare che i concetti si esprimono mediante parole e che il nostro cervello ha dei significati profondamente radicati, in quanto basici in senso vitale. Parole come spazio e tempo rappresentano preconcetti registrati a livello molto basso o nel profondo del nostro cervello.
Ovvio, già che ci siamo non relativizziamo solo i riferimenti dello spazio ma anche lo spazio stesso.
Siccome tutto questo non bastava, c’è stato bisogno di aggiungere una spiegazione, con l’idea della relatività della percezione del tempo per gli esseri viventi, compresi gemelli, o, se si preferisce, la relatività del tempo soggettivo. Ci hanno persino messo di mezzo l’amore, immagino affinché fosse più convincente. Vediamo chi nega che …!
Siccome esiste effettivamente questa percezione o questa realtà soggettiva, hanno finito per accettare un modello scientifico che dice che se due oggetti si allontanano, ognuno di loro alla velocità della luce, la velocità alla quale si separano è sempre quella della luce, come nell’esperimento dei fotoni antipodi.
Un elemento addizionale è che tutto è molto relativo e che quando interessa, perché c’è qualcosa che non torna, si può dire: "Va bene, effettivamente il tema è molto più complesso, ma stavamo facendo una semplificazione implicita per … te."
Per di più, in caso di bisogno ti rimandano ai tensori delle formule della Relatività Generale e … luci spente!
Perché non si spiega che la relatività del tempo significa una conversione asintotica della velocità della luce affinché non oltrepassi c e che si deduce semplicemente dal teorema di Pitagora? O ancora più semplice, che la ragione del piegamento e dello spiegamento temporale è l’inverso del coseno dei lati corrispondenti del triangolo rettangolo. Mi riferisco alla ragione o proporzione matematica, non alla ragione logica, a meno che la prima non implichi la seconda.
Scoperta in Grecia del teorema di Pitagora
Se si ritiene complicata la fisica relativista, facciamo un esercizio su come deve essere stato scoperto in quei tempi e in cosa consiste il teorema di Pitagora, ipotizzando che conoscessero le buste per mandare la posta ed un po’ di meccanica.
Il trucco consiste nel pensare che la busta è aperta e chiusa allo stesso tempo, come se fosse una busta quantica, e nell’osservare bene la curvatura geometrica dell’aletta nel girare dentro il quadrato grande B (lato=b), stendersi, espandersi o venire fuori per formare il quadrato piccolo A (lato=a).
Come si può facilmente osservare, l’area di B è il doppio di quella di A. Allora, siccome l’area di B è b² e quella di A è a²; abbiamo [b² = a² + a²] e trovando la radice quadrata otterremo il teorema di Pitagora.
Área de A = a² = b² / 2
Una curiosità matematica molto comune a scuola, questa volta con lo stesso teorema di Pitagora e non legata alla Teoria della Relatività di Einstein, è quando insegnano che per calcolare l’area di un quadrato conoscendone la diagonale, ti dicono che bisogna calcolare il lato con il teorema di Pitagora e poi elevarlo al quadrato, anziché dire che è uguale alla diagonale al quadrato diviso due.
Un’applicazione concreta del teorema di Pitagora alla Relatività Speciale è presente nella figura dell’esperimento mentale di Ipotesi irreali o contraddittorie.
In tale esempio si mostra il triangolo rettangolo che si formerebbe in seguito alla diversa prospettiva dei due osservatori e viene indicata l’idea implicita che la luce conserva l’inerzia della nave spaziale, ma solo un ipotetico osservatore lo percepisce …
Teorema di Pitagora 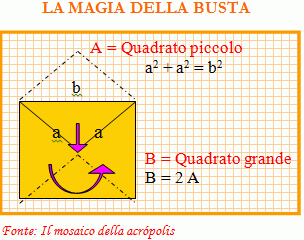
La figura menzionata è del tutto simile all’ipotesi discussa parlando dell’elemento della relatività del tempo, da cui è stato dedotto che la differenza temporale si poteva facilmente calcolare, essendo:
t = t0 /(1 - v²/c²)½
Scoperta in America della Relatività Speciale
Effettivamente, un piccolo calcolo basato sul moderno teorema di Pitagora, in cui i cateti e l’ipotenusa sono spazi percorsi dalla luce e dall’oggetto in movimento relativo visti da diversi osservatori immaginari e opportunamente mescolati ci dà il risultato mostrato prima.
Per facilitare l’assimilazione di quanto detto, mostriamo le seguenti equazioni che consentono di farsi un’idea immediata di com’è la cosa del tempo pitagorico e che, a causa della difficoltà a capirlo e ad ammetterlo e dei neuroni terrorizzati di mezzo mondo, si potrebbe esprimere come tempo fantasmagorico.
Bisogna normalizzare l’ipotenusa del triangolo per c o velocità della luce. Se le velocità u e c sono uguali perché sono quelle della luce, mentre v è quella della nave spaziale, la dilatazione del tempo dovrà dunque essere proporzionale all’inverso del coseno dell’angolo α.
Se la luce incorporasse l’inerzia per un osservatore si dovrebbe concludere che penserebbe che ci troviamo di fronte al tipico caso di sistemi inerziali con velocità additive, tranne che fosse un osservatore del zigzag ma inconsapevole del suo significato.
Deduzione analitica Teorema di Pitagora u² = c² - v² Normalizzazione c² u² / c² = 1 - v²/c² Radice quadrata e resta Cos α = u / c = (1 - v²/c²)½ Risolvere c c = u * (1 - v²/c²)-½ Sostituire costante ausiliare γ
di Lorenzc = u * γ Come vedremo più avanti, non sarebbe molto lontano dalla visione della realtà che si propone coscientemente!
Si introducono poi le trasformazioni di Lorentz per allontanare il fantasma di Pitagora. Da notare tuttavia la similitudine delle due forme che prende il Cos α con le due costanti ausiliari delle suddette equazioni.
E visto che ci siamo si potrebbe dire che il teorema di Pitagora è un’applicazione particolare del caso concreto del teorema di Talete quando c’è un angolo retto, insomma, fatti l’uno per l’altro.
Inoltre è risaputo che il teorema fondamentale della trigonometria, seno per seno più coseno al quadrato è uguale a uno, è un’implicazione elementare del teorema di Pitagora; dato che sia la quantificazione del seno che quella del coseno è effettuata per definizione prendendo come unità l’ipotenusa, cioè il numero di ipotenuse nel cateto contiguo o cateto opposto all’angolo in questione.
Almeno si dice che il viaggio a ritroso nel tempo non è possibile. Meno male, perché sarebbe un’audacia suprema. Ciò che non spiegano molto bene è come, dopo un lasso di tempo relativo, si torni al tempo normale. Sospetto che bisognerà ricorrere alle tensioni della Relatività Generale!
Il pandemonio che si può scatenare con il giocomonio con il tempo è apocalittico, fatti simultanei per osservatori intelligenti che non sono simultanei per un altro tipo di osservatori, spazi che si allungano, effetti geometrici che stimolano l’immaginazione, ecc.
