4.b.2. Curvatura de la luz del efecto de las lentes gravitacionales
La predicción sobre el comportamiento de las estrellas como lentes gravitacionales en la curvatura de la luz es la primera de las tres predicciones de la Relatividad General y fue muy famosa por el retraso en su confirmación experimental hasta el eclipse solar de 1919.
También influye en la fama de esta predicción el que suponga un efecto de lupa gravitacional sencillo de visualizar y que la curvatura de la luz predicha por el efecto de lente gravitacional y confirmada era justo el doble de la que resultaría de aplicar la Ley de la Gravitación Universal de Newton.
Resulta curioso que el continuum espacio-tiempo se estire-dilate en la curvatura de la luz por el efecto de lentes gravitacionales en el factor *2* respecto a lo previsto por la Ley de Gravitación de Newton y nadie parezca saber cuál es la razón física, sobre todo porque el número es bastante redondo y sencillo. Por supuesto, la remisión es sistemática a las ecuaciones de campo de Einstein, pero nada más.
Buscando en Internet –ver artículo bending Light en mathpages.com **– o preguntando a cualquier amigo que de verdad sepa algo de matemáticas y geometría elíptica, éste le dirá que una partícula que pasa cerca del Sol describe una hipérbole por actuar éste como lente gravitacional y que, en función de su excentricidad, para valores muy pequeños de m respecto r0 y según la Ley de Gravitación de la mecánica newtoniana, el ángulo o curvatura total de la luz sería igual a:
α = 2 m /r0 = 0,875'' de arco
Donde m es la masa del Sol en unidades geométricas –la masa multiplicada por G o constante de gravitación y dividida por la velocidad de la luz al cuadrado– y r0 la distancia más próxima del rayo de luz al Sol.
Recordando un poco de la geometría de un círculo, una vuelta entera tiene 360º grados, cada grado tiene 60' minutos y cada minuto 60'' segundos de arco.
Por lo tanto, el ángulo o curvatura de la luz que provocarían las lentes gravitacionales en la Ley de la Gravitación Universal de Newton es directamente proporcional a la masa que crea el campo de gravedad, al ser la fuerza centrípeta directamente proporcional a la masa.
Aunque un planeta tiene masa, en Mecánica Clásica no se tiene en cuenta dicha masa, puesto que se ejerce una fuerza gravitatoria sobre el planeta en función de su masa gravitacional; la fuerza por unidad de masa gravitacional permanecerá constante incluso si se tuviese en cuenta la masa cinética –masa equivalencia a la energía cinética.
Ahora bien, con la Ley de la Gravedad Global existe una fuerza adicional, la segunda componente de la atractis causa o efecto Merlín se debe a la velocidad y opera sobre la misma masa cinética. La masa global es la masa en reposo más la masa equivalente a la energía cinética. En el caso de la luz la masa en reposo no existe.
En el apartado de la Ley de la Gravedad Global de este libro se ha comentado que dicha ley debería estar expresada en términos de energía y no de masa, puesto que la interacción gravitatoria se produce por transferencia entre la energía del campo de gravedad y la energía elástica en forma de masa, de masa cinética o de energía electromagnética.
Para calcular la curvatura de la luz en el efecto de lentes gravitacionales sobre la energía electromagnética, solo nos queda verificar que la segunda componente o fuerza de gravedad adicional derivada de la velocidad es igual cuantitativamente a la primera componente.
Intuitivamente es sencillo, puesto que el valor de la energía cinética de la luz será igual a la supuesta masa cinética equivalente.
Anillo Einstein - NASA (Imagen de dominio público)

Desde otra perspectiva, si la primera componente de la atractis causa es debida a la velocidad de la propagación de la tensión longitudinal del Éter Global y ésta es igual a la velocidad de la luz, como la segunda componente –efecto Merlín– es debida la velocidad de la luz para el caso de la energía electromagnética, las dos componentes de la atractis causa tendrán el mismo valor y la curvatura de la luz por las lentes gravitacionales será el doble que la que obtendríamos con la Ley de Gravitación de Newton.
La explicación anterior de la causa física del efecto de lentes gravitacionales o curvatura de la luz es un resumen de lo comentado en el apartado segundo de este libro y en los apartados sobre el movimiento con simetría total y con simetría radial de la gravedad en el libro Física y Dinámica Global.
No obstante, para los aficionados a las matemáticas se incluye el siguiente análisis cuantitativo que, además de tener cierto valor educativo, es, de alguna manera, común a la Física Global y a la Relatividad General.
ANÁLISIS CUANTITATIVO
Ya he comentado que el incremento de la masa con la velocidad es un aspecto parcialmente correcto de la Teoría de la Relatividad –si se introduce el sistema de referencias natural para la velocidad física– y, en consecuencia, este concepto se mantiene en la Física Global; basado, en este último modelo, en la pura observación experimental y en los mecanismos de la transferencia energética de la interacción gravitatoria, en contraposición a la imposición de axiomas matemáticos en la Física Moderna.
Dicho de otra forma, no es necesario mantener la Teoría de la Relatividad para aceptar el citado incremento de la masa física con la velocidad.
La conocida fórmula de la masa global que sirve para deducir la energía cinética en términos relativistas es la siguiente:
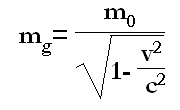
masa global = masa en reposo + masa cinética
[2.a] m = m0 /(1 - v²/c²)½
O de forma abreviada,
m = γ m0
Como señala la propia Teoría de la Relatividad de Einstein, la energía cinética será equivalente al incremento de la masa en reposo m0
El desarrollo en serie del teorema de Taylor de la constante γ nos da:
γ = 1+½ v²/c² +3/8 v4/c4+5/16 v6/c6+...
Energía cinética = m0 [ ½ v²/c² +3/8 v4/c4+5/16 v6/c6+...]
A estos efectos la ecuación relevante de la masa global no debe contener la simplificación realizada para la energía cinética clásica en el desarrollo en serie del teorema de Taylor, puesto que el segundo término del paréntesis se vuelve significativo para velocidades del orden de la luz.
Como buen Einsotro, aquí pregunté a un amigo mensista, que estaba haciendo ciencias exactas en la universidad, y me contestó que él pasaba de calcular derivadas terceras, desde luego, yo le comprendo y sigue siendo amigo.
Al margen de anécdotas simpáticas, en el desarrollo en serie del teorema de Taylor solo son válidos los términos correspondientes a las derivadas de la función siempre y cuando dichas derivadas existan, es decir, sean distintas de cero. En general, matemáticamente en la igualdad anterior se calcula el último término válido de forma que recoja los términos eliminados.
En nuestro caso, si acumulamos ( 1/8v4/c4 ) al segundo término recogeremos el efecto residual del resto de términos eliminados y nos quedará:
Energía cinética = m0 [½ v²/c²+½ v4/c4]
Lógicamente el primer término del paréntesis se puede despreciar para velocidades bajas o no planetarias, mientras que el segundo término se podrá despreciar para planetarias pero no para velocidades de orden cercano al de la luz y mucho menos para la velocidad similar al caso de lentes gravitacionales. Consiguientemente, en un análisis general se han de tener en cuenta todas las posibilidades del valor de la velocidad de la masa física para determinar la fuera de gravedad total.
A mayor abundamiento, en la ecuación (2) de la página en inglés de Mathpages.com ** sobre la inercia de la energía tenemos la utilización de este mismo desarrollo en serie del teorema de Taylor.
(Velocidades cercanas a la luz)

La demostración de la Relatividad General de que el efecto de lentes gravitacionales es doble respecto a la Ley de Gravitación de Newton es bastante compleja; pero parece que inevitablemente también se utiliza el mismo desarrollo en serie del teorema de Taylor, como se puede ver en la página sobre la curvatura de la luz del sitio de Mathpages.com citado anteriormente.
Por el contrario, sin contar el desarrollo en serie de Taylor, en la Física Global el cálculo no puede ser más sencillo.
Luego, el ángulo de la curvatura de la luz por el efecto de las lentes gravitacionales será el doble del que predice la Ley de la Gravitación Universal de la teoría de Newton, como ya sabíamos por las famosas observaciones del eclipse del Sol de 1919 y posteriores, siendo 1,75'' de arco.
