2.c.2.a) Teorema de Pitágoras y Relatividad de Einstein
La Teoría de la Relatividad Especial se asocia una gran complejidad matemática, pero pienso que la complejidad es mucho más conceptual que matemática, ya que básicamente consiste en la aplicación del teorema de Pitágoras.
-
No hay que olvidar que los conceptos se expresan mediante palabras y nuestro cerebro tiene muy arraigados algunos significados por ser muy básicos en sentido vital. Palabras como espacio y tiempo conforman preconceptos grabados a muy bajo nivel o muy profundamente en nuestro cerebro.
Claro, de paso, no solo se relativizan las referencias del espacio sino también el espacio mismo.
Como no era suficiente todo lo anterior, fue necesario añadir una explicación con la idea de la relatividad de la percepción del tiempo por los seres vivos, incluso gemelos; o si se prefiere, la relatividad del tiempo subjetivo. Hasta se metió el amor por medio, supongo, para que fuese más convincente. ¡A ver quién niega que...!
Al existir efectivamente esa percepción o esa realidad subjetiva se acabó aceptando un modelo científico que dice que si dos objetos se alejan cada uno a la velocidad de la luz, la velocidad a la que se separan sigue siendo la de la luz, como en el experimento de los fotones antípodos.
Un elemento adicional es que todo es muy relativo y cuando interesa, porque algo no cuadra muy bien, se puede decir: “Bueno, efectivamente el tema es mucho más complejo, pero estábamos haciendo una simplificación implícita para... ti.”
Además, en caso de necesidad te remiten a los tensores de las fórmulas la Relatividad General y... ¡se apagó la luz!
¿Por qué no se explica que la relatividad del tiempo significa una conversión asintótica de la velocidad de la luz para que no sobrepase c y que se deduce sencillamente del teorema de Pitágoras? O todavía más sencillo, que la razón del pliegue o despliegue temporal es el inverso del coseno de los lados correspondientes del triángulo rectángulo.
Descubrimiento en Grecia del teorema de Pitágoras
Por si se considera complicada la física relativista, vamos a hacer un ejercicio de cómo se debió descubrir en su época y en qué consiste el teorema de Pitágoras, suponiendo que conocieran el sobre de enviar correos y un poco de mecánica.
El truco consiste en pensar que el sobre está abierto y cerrado al mismo tiempo, como si se tratase de un sobre cuántico, y en fijarse en la curvatura geométrica de la solapa al girar dentro del cuadrado grande B (lado=b), desdoblarse, expandirse o salirse para formar el cuadrado pequeño A (lado=a)
Como se puede observar con facilidad, el área de B es el doble que la de A. Entonces, como el área de B es b² y el de A es a²; tenemos que [b² = a² + a²] y sacando la raíz cuadrada obtenemos el teorema de Pitágoras.
Área de A = a² = b² / 2
Una curiosidad matemática muy común en los colegios, esta vez con el propio teorema de Pitágoras y no relacionada con la Teoría de la Relatividad de Einstein, es cuando enseñan que para calcular el área de un cuadrado sabiendo su diagonal, te dicen que se tiene que calcular el lado con el teorema de Pitágoras y luego elevarlo al cuadrado; en lugar de decir que es igual a la diagonal al cuadrado partido por dos.
Una aplicación concreta del teorema de Pitágoras a la Relatividad Especial se recoge en la figura del experimento mental de Hipótesis irreales o contradictorias.
Teorema de Pitágoras 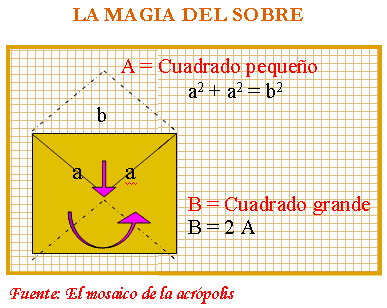
En dicho ejemplo se muestra el triángulo rectángulo que se formaría por la diferente perspectiva de dos observadores y se indica la idea implícita de que la luz conserva la inercia de la nave espacial, pero solo un hipotético observador percibe el tema...
La citada figura es totalmente similar al supuesto comentado al hablar del elemento de la relatividad del tiempo, de donde se dedujo que la diferencia temporal se podía calcular fácilmente, siendo:
t = t0 /(1 - v²/c²)½
Descubrimiento en América de la Relatividad Especial
Efectivamente, un pequeño cálculo basado el moderno teorema de Pitágoras, donde los catetos y la hipotenusa son espacios recorridos por la luz y por el objeto en movimiento relativo vistos por distintos observadores imaginarios y convenientemente mezclados nos da el resultado anteriormente mostrado.
Para facilitar la asimilación de lo anterior, se muestran las siguientes ecuaciones que permiten hacerse una idea inmediata de por dónde van los tiros del tiempo pitagórico y que, por la dificultad en entenderlo y reconocerlo y por tener aterradas a las neuronitas de medio mundo, se podría expresar como tiempo fantasmagórico.
Se trata de normalizar la hipotenusa del triángulo por c o velocidad de la luz. Si la velocidad u y c son iguales porque son las de la luz, mientras que v es la de la nave espacial, tendremos que la dilatación del tiempo deberá ser proporcional al inverso del coseno del ángulo α.
Deducción analítica Teorema de Pitágoras u² = c² - v² Normalización c² u² / c² = 1 - v²/c² Raíz cuadrada y queda Cos α = u / c = (1 - v²/c²)½ Despejar c c = u * (1 - v²/c²)-½ Sustituir constante auxiliar γ
de Lorenzc = u * γ Si la luz incorporase la inercia para un observador habría que concluir que él pensaría que nos encontraríamos ante el típico caso de sistemas inerciales con velocidades aditivas, salvo que fuese un observador del zigzag, pero inconsciente de su significado.
¡Cómo veremos más adelante, no estaría muy lejos de la visión de la realidad que conscientemente se propone!
Después se introducen las transformaciones de Lorentz para alejar el fantasma de Pitágoras. No obstante, nótese la similitud de las dos formas que toma el Cos α con las dos constantes auxiliares de dichas ecuaciones.
Ya puestos, se podría decir que el teorema de Pitágoras es una aplicación particular del caso concreto del teorema de Tales cuando existe un ángulo recto; en fin, tal para tal.
También es de sobra conocido que el teorema fundamental de la trigonometría, seno por seno más coseno al cuadrado igual a uno, es una implicación elemental del teorema de Pitágoras; dado que tanto la cuantificación del seno como del coseno se realiza por definición tomando la hipotenusa como unidad, es decir, el número de hipotenusas en el cateto contiguo o cateto opuesto al ángulo en cuestión.
Al menos, se dice que el viaje en el tiempo hacia atrás no es posible. Menos mal, porque sería un atrevimiento supremo. Lo que no explican muy bien es cómo, después de un lapsus de tiempo relativo, se vuelve al tiempo normal. ¡Sospecho que hará falta tirar de las tensiones de la Relatividad General!
El fogón que se puede armar con los jogos con el tiempo es apoteósico, sucesos simultáneos para observadores inteligentes que no son simultáneos para otro tipo de observadores, espacios que se alargan, efectos geométricos que estimulan la imaginación, etc.
