El espacio-tiempo y la velocidad

2.c.2) Relación espacio-tiempo y velocidad

El concepto de espacio-tiempo o continuum del espacio-tiempo surge al invertir la definición de velocidad. La velocidad ya no es la relación entre el espacio y el tiempo, sino que existe un máximo y, en consecuencia, el espacio y el tiempo empiezan a depender el uno del otro para que la velocidad de la luz sea constante. Dicho concepto interdependiente configura la naturaleza del espacio-tiempo en la Teoría de la Relatividad de Einstein.

Pero vayamos mejor por partes...

• Relatividad de tiempo.

  La ley de relatividad del tiempo surge de la interpretación que se da al experimento de Michelson-Morley, si se recorren dos espacios diferentes simultáneamente con la misma velocidad lo único que se puede hacer para no perderse del todo es hacer el tiempo relativo, efecto conocido como dilatación del tiempo.

  En la Teoría de la Relatividad, el tiempo t₀ que mide un observador con un reloj en reposo de eventos ocurridos en su mismo lugar recibe el nombre de tiempo propio del intervalo entre eventos.

  Un ejemplo típico de los libros para explicar el concepto de espacio-tiempo y la denominada dilatación del tiempo consiste en un ejemplo de un reloj óptico montado en una nave espacial y otro fijo en la tierra. Más abajo se discute el experimento mental sobre la teoría del espacio-tiempo en profundidad.

  Desde la tierra, un observador vería que el rayo de luz del reloj óptico va en zigzag por el movimiento de la nave, mientras que el reloj de la tierra va directamente de arriba abajo.

  En consecuencia, dada la diferencia de distancia recorrida por la luz y su velocidad constante, debemos concluir que el tiempo es diferente para cada uno de los observadores, esta diferencia o dilatación del tiempo la podemos calcular fácilmente, siendo:

  t = t₀ * (1 - v²/c²)-½

  Obviamente, el experimento mental sobre la estructura del espacio-tiempo es generalizable a relojes comunes y la dilatación del tiempo está súper probada. Como dice un libro concreto: "...confirman esta respuesta cálculos detallados sobre lo que ocurre a relojes comunes en movimiento, visto desde la Tierra".

  El concepto de relatividad del tiempo tiene varias implicaciones. Un ejemplo importante es que el concepto de simultaneidad también resulta relativo y hasta el principio de conservación de la energía ha de ser reformulado para mantener su vigencia. En el libro Experimentos de Física Global se proponen varios experimentos científicos sobre la medición del tiempo y, en particular, el experimento del Tren de la Abrujuela sobre el problema de la simultaneidad.

  Con relación a la cuestión de los viajes en el tiempo, la dilatación del tiempo no corre para atrás para ningún observador, aunque algunos científicos cuántico-relativistas tratan de conseguir lo contrario.

  La paradoja de los gemelos (relojes ópticos, normales o personas) viene a complicar la filosofía del espacio-tiempo por el problema de cuál de los observadores estará en lo cierto, pues el efecto de la dilatación del tiempo del observador en la Tierra sobre el reloj en la nave espacial lo tendría de forma totalmente simétrica el observador en la nave espacial de un reloj en la Tierra.

  La imaginaria solución de la paradoja de los gemelos viene dada por la aplicación de la Relatividad General. La mecánica relativista nos dice que los sistemas de referencia acelerados son no inerciales y habría que tener en cuenta que la nave espacial ha sido acelerada y desacelerada varias veces y ha permanecido en distintos sistemas de referencia inerciales por las sucesivas aceleraciones.

  En este mismo libro existe una página dedicada a la Paradoja de los gemelos, donde se explica que ni tiene solución ni puede tenerla dentro de la física relativista.

  Otra forma algo más complicada de deducir la supuesta naturaleza relativista del espacio-tiempo o la relatividad del tiempo es mediante las ecuaciones de las transformaciones de Lorentz. Éstas eran consideradas un juego matemático hasta que Albert Einstein descubrió su verdadera significación.

  Las transformaciones de Galileo deben ser sustituidas por las ecuaciones de Lorentz para que se cumplan los dos postulados de la Relatividad Especial: la expresión de las leyes físicas no se verá alterada y la velocidad de la luz será la misma para todos los observadores.

• Relatividad del espacio.

  Las medidas del espacio pueden ser relativas respecto a cualquier punto, pero no existe un origen universal del espacio, o éste no es conocido.

  Aquí aparece de nuevo el principio de que todo movimiento es relativo, pero la relación entre el espacio y el tiempo relativista no se refiere a este hecho sino al efecto de contracción del espacio en función de si la velocidad se mide en un sistema de referencia u otro.

  En otras palabras, un metro no siempre implica el mismo espacio, depende del observador y su velocidad relativa, lo único que permanece constante con la filosofía de la curvatura del espacio y el tiempo es la velocidad de la luz o relación espacio-tiempo.

  Este concepto de relatividad del espacio se deduce del experimento mental del reloj óptico cuando el rayo de luz se mueve en la dirección de la nave espacial y, por supuesto, de la interpretación ortodoxa del experimento de Michelson-Morley.

  La hipótesis de la contracción de los objetos en movimiento se denomina contracción de Fitzgerald-Lorentz y es similar y complementario al de tiempo, depende del eje del espacio-tiempo que se considere afectado en el movimiento relativo entre los sistemas de referencia, el del tiempo o el del espacio.

  Si se considera solo la alteración del espacio quedaría:

  L₀ = x'₂ - x'₁
  L = L₀ / γ

  Donde la relación de transformación sigue dependiendo de γ, en concreto de su inverso. En el caso de afectar a ambos ejes, únicamente se complicarían las fórmulas matemáticas pero los razonamientos serían similares.

El libro Física y Dinámica Global profundiza en el análisis del movimiento de la luz dentro de la nueva teoría del todo. La Física Global asume una filosofía del tiempo y el espacio de naturaleza absoluta.

Veamos ahora una explicación detallada del experimento-ejemplo mental del reloj óptico de la Teoría de la Relatividad.

En este caso la descripción de la realidad física es, a mi juicio, equivocada porque incorpora implícitamente la inercia a la luz. Cosa que me llama mucho la atención porque precisamente un concepto que se maneja mucho en esta materia es el de sistemas inerciales y no inerciales.

Otro aspecto muy intrigante y que ciertamente asusta un poco, es que, si utilizan un experimento mental, será porque no tienen ningún experimento físico más apropiado. Yo también diría que la realidad no es como se dibuja en el experimento mental siguiente:

• Hipótesis irreales o contradictorias

  "En una nave espacial, se dispara un rayo de luz en dirección perpendicular a la dirección de la nave, el rayo chocará con un espejo y volverá hacia el punto inicial, un observador en la nave verá los caminos de ida y vuelta en dirección perpendicular al desplazamiento de la nave. Por el contrario, como la nave se desplaza a gran velocidad, un observador desde la Tierra verá el movimiento de la luz en zigzag; es decir, para él la distancia recorrida es mayor que la del observador en la nave".

  Yo considero que la velocidad de la luz en la Tierra es aditiva respecto a la del campo de gravedad de la Tierra, pero no respecto a la de un tren. En el espacio exterior pasará lo mismo respecto a su campo de gravedad –Éter LUM (Luminífero, universal y móvil) –, pero no respecto a la nave espacial.

  El resto es fácil, si se admite la constancia de la velocidad de la luz y se supone la inercia vectorial en su trayectoria de ida y en el recorrido de vuelta, la distancia recorrida será mayor en la nave espacial que en la Tierra. Entonces, la única solución posible será hacer relativo el tiempo e inventar la naturaleza del espacio-tiempo relativista.

  Aquí nos volvemos a encontrar con un triángulo rectángulo, el tiempo se habrá dilatado lo suficiente para que, con una velocidad constante, el cateto correspondiente al espacio inicial (a) se iguale a la hipotenusa (c). Es decir, la ratio de dilatación temporal será el inverso del coseno del ángulo formado por dichos lados, o lo que es lo mismo (c /a) que coincide con la primera variable auxiliar de las ecuaciones de Lorentz; o también igual al inverso de la raíz cuadrada de (1 - b²/c²), como se deduce del teorema de Pitágoras y que además coincide con la segunda variable auxiliar de las transformaciones de Lorentz.

  

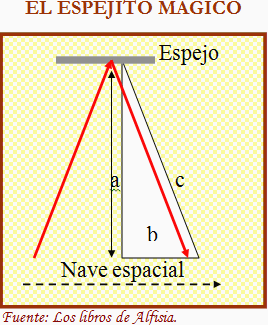
  La verdad es que dan ganas de preguntar: "Espejito mágico, espejito mágico, ¿cuál es la teoría más bonita?"

  Además, me temo que si tuviésemos más observadores o espejos obtendríamos más triángulos con algún lado en común y tendríamos que relativizar lo relativo. Imagínense la curvatura del espacio-tiempo que podríamos conseguir con un par de hexágonos grandes.

  Otros ejemplos que he visto en libros de relatividad de cruzar un río con una barca y tener en cuenta el movimiento de la corriente son similares al que acabamos de exponer sobre la nave espacial y la estructura del espacio y el tiempo.