2.c) Concepto, postulados y elementos de la Teoría de la Relatividad Especial
La Teoría de la Relatividad Especial, presentada por Albert Einstein en 1905, trata los temas relacionados con el marco de referencia. Los sistemas de referencia inerciales son los que se mueven a velocidad constante unos con respecto a otros o movimiento relativo uniforme.
Esta teoría realizó una integración de numerosas ideas que circulaban por la época y supuso el definitivo abandono de la idea de la existencia del Éter LUM (Luminífero, universal y móvil) , con las implicaciones derivadas sobre la naturaleza de la luz y la asunción de la ley de la relatividad del tiempo y el espacio, tal y como se conoce hoy en día.
Como se explica a continuación en un breve apunte, además de los elementos de la ley de la relatividad del espacio y el tiempo Einstein incorporó la novedad de la equivalencia entre masa y energía, es decir, el concepto de la masa relativista y la base de la bomba atómica.
Los dos postulados en que se basa la Teoría de la Relatividad Especial son:
Las leyes físicas se pueden expresar mediante ecuaciones que tienen la misma forma en todos los sistemas de referencia que se mueven a velocidad constante unos con respecto a otros.
La velocidad de la luz en el espacio libre tiene el mismo valor para todos los observadores, independientemente de su estado de movimiento.
Una de las críticas más fuertes desde el punto de vista formal es que la RE es una teoría ad hoc y posteriormente la RG tiene esta misma característica, pues se desarrolló para medio solventar los fallos insalvables de la primera, como la paradoja de los gemelos. De hecho, si la RG resuelve esta paradoja es porque solo da soluciones locales y un gemelo no puede alejarse demasiado.
Traje a medida de las interpretaciones matemáticas
Todos los intentos por explicar la naturaleza de la velocidad de la luz no acababan de cuajar. Entonces Einstein recogió una serie de conocimientos de la época y los encajó en un conjunto más o menos coherente. Esto es algo correcto, pero de acuerdo con el método científico debilita una teoría en cuanto a su consistencia interna.
Una pieza fundamental serían las ecuaciones de Lorentz y su especial interpretación de los marcos o sistemas de referencia inerciales con un máximo en la velocidad de la luz c. Como resolvían muchos problemas y eran francamente cómodas, como buen sastre, se hizo una teoría a su medida.
El primer postulado o ley de la Teoría de la Relatividad Especial básicamente se refiere a "... ecuaciones que tienen la misma forma...", y el segundo a "La velocidad de la luz en el espacio libre tiene el mismo valor para todos los observadores..."
El primer postulado de la relatividad es una exposición de lo que implican en sí mismas las ecuaciones de Lorentz, que no cambian en los diferentes sistemas de referencia u observadores inerciales. Sin embargo, lo que sí cambia es la definición de las variables internas, como el tiempo, que pasa de ser una función monótona creciente y exógena a una función endógena y asintótica...
La segunda ley de la relatividad todavía es más pobre. Este postulado relativista dice lo que matemáticamente hacen dichas ecuaciones, que la velocidad de la luz es siempre la misma en cualquier marco de referencia o para cualquier observador inercial.
¡Sólo faltaba que después de hacer la transformación asintótica desde cualquier sistema de referencia fuese diferente! Es de suponer que al método científico no le gustan las ecuaciones que fuerzan un resultado artificialmente y después se dice que está demostrado en múltiples experimentos.
De hecho, Einstein podría haber dicho: "Mi teoría son los postulados de Poincaré expresados por las ecuaciones de Lorentz..., y conozco el experimento de Michelson-Morley."
El resto de conclusiones e implicaciones de la teoría de Einstein vienen como consecuencia de todo el juego matemático subsiguiente apoyado por el fracaso del experimento de Michelson-Morley en relación a su objetivo previsto y de la existencia real física del incremento de la masa con la velocidad relativa al marco o sistema de referencia natural en una cantidad equivalente a la que se deduce de las ecuaciones de Lorentz.
El primer apoyo, conocido con anterioridad a la formulación de las leyes de la Relatividad Especial, se comenta con detalle en la página Experimento Michelson-Morley.
El segundo, respecto a la masa relativista, era muy sospechado como se señala en el apartado de la crítica de la masa relativista, puesto que había experimentos físicos que apuntaban en dicha dirección. No obstante, el aumento de masa física únicamente es cierto cuando se mide el movimiento respecto al sistema de referencia privilegiado o natural como se explican en el apartado de Física del movimiento en gravedad del libro Física y Dinámica Global.
Por otra parte, como también se discute en dicho libro, el aumento de masa con la Energía cinética es cierto, pero además afecta a la configuración espacial del conjunto de la masa.
Nótese que no quiero entrar en detalles técnicos de si la masa aumenta, cumpliéndose literalmente la segunda Ley de Newton y manteniéndose o no el principio de igualdad entre masa inercial y gravitatoria, o si la masa es invariante y todo ha de entenderse con la debida adaptación lorentziana.
Veamos a continuación tanto los elementos citados anteriormente como algunos elementos terminológicos importantes de la Relatividad Especial.
2.c.1. Marco o sistema de referencia
Cualquier método o mecanismo de medida necesita un sistema de referencia, un punto origen sobre el que basar las diferentes mediciones, incluso por la lógica humana todos los conceptos son relativos, todos necesitan su contrario, su complementario respecto al todo, etc. Es la forma de razonar y facilitar el pensamiento. Podríamos decir que es la consecuencia del principio tautológico de que todo movimiento es relativo.
Este tema surge en la escala en que nos movemos con la problemática de la Mecánica Clásica en cuanto al principio de relatividad de Galileo Galilei, del siglo XVII, que dice que cualquier experimento mecánico tendrá las mismas características en un sistema en reposo que en uno con velocidad constante respecto al primero.
En definitiva, se trata de los conceptos clásicos de fuerza, masa, espacio y tiempo con todas las transformaciones correspondientes al cambiar el sistema o marco de referencia.
El sistema clásico funcionaba perfectamente hasta la aparición del electromagnetismo y la naturaleza de la luz con su velocidad no aditiva respecto a su fuente.
El sistema de referencia espacial no tiene ningún secreto, un punto se puede determinar fácilmente dentro de su marco de referencia o cambiar de sistema de referencia mediante un ajuste del origen del nuevo sistema respecto del primero en cada instante o momento.
Las magnitudes correspondientes de un sistema de referencia a otro se pueden obtener con sencillez a partir de las transformaciones de Galileo. Dados dos sistemas de referencia inerciales S y S', las ecuaciones normales serán:
Esta equivalencia de mediciones es todavía más simple e inmediata, desde luego, con la aparición de los ordenadores modernos y sus potentes cálculos.
y' = y
z' = z
Por supuesto t' = t
Gracias a ellos se puede mantener el comentario de la facilidad de las transformaciones bajo el principio de la relatividad de Einstein y las ecuaciones de Lorentz, ya comentadas.
Sistemas de referencia inerciales y no inerciales.
Cuando los marcos de referencia se mueven con velocidad constante unos respecto de otros, se denominan sistemas de referencia inerciales. En caso contrario, lógicamente, se denominan sistemas de referencia no inerciales. Todos los sistemas de referencia no inerciales están acelerados unos respecto a otros.
En la Mecánica Clásica, las magnitudes citadas de fuerza, masa, espacio y tiempo no cambian al pasar de un sistema de referencia inercial a otro y por ello reciben el nombre de invariantes de Galileo.
El marco de referencia no inercial es aquél en que la inercia no sigue los principios o comportamientos clásicos, básicamente la segunda ley de Newton o ley fundamental de la dinámica relativa a la proporcionalidad entre fuerza y aceleración representada por la masa de un cuerpo y a la tercera ley de Newton o principio de acción y reacción.
En un sistema no inercial siempre existirán fuerzas que soporten la aceleración y aparecerán las denominadas fuerzas ficticias porque no responden al principio de acción y reacción.
En la mecánica relativista, en los sistemas de referencia inerciales la masa varía con la velocidad y también varía con el simple cambio de sistema de referencia no inercial. Una fuerza constante no produce una aceleración constante; este efecto será muy importante cuando la velocidad empieza a ser comparable a la de la luz, es el efecto de la llamada masa relativista.
Veamos a continuación dos errores de concepto que creo se cometen en esta materia.
La independencia del observador
La Relatividad Especial se plantea como una teoría que simplifica la realidad al señalar que las leyes físicas se pueden expresar mediante ecuaciones que tienen la misma forma y que la velocidad de la luz en el espacio libre tiene el mismo valor para todos los observadores.
Es interesante ver cómo en la práctica esos planteamientos formales se traducen en una complejidad inmensa, tanto que la realidad pasa a depender de cada observador. La ley de la relatividad del tiempo y del espacio se traduce en una variabilidad que afecta a las unidades de fuerza y energía.
Todas las medidas y unidades del Sistema Internacional de Unidades (SI), también denominado Sistema Internacional de Medidas, se ven afectadas por la velocidad y la situación en el campo gravitatorio de cada observador. Además, se pretende que todo el aparato matemático que se utiliza es real y no virtual.
Hay que tener cuidado con el concepto de realidad porque todavía no he visto ningún número andando por la calle.
Yo me pregunto, si se saben todas las relaciones entre las variables del modelo, ¿por qué no se utiliza ese conocimiento para generar un sistema de unidades estable que permita una visión intuitiva de la realidad? ¿Qué interés existe en que no se entienda nada?
Ya he comentado en la definición de segundo, si se sabe perfectamente cómo afecta la gravedad a los relojes atómicos: ¿por qué se define el segundo en función de dichos relojes sin fijar unas condiciones concretas de intensidad del campo gravitatorio?
La Teoría de la Relatividad de Einstein, además de incorrecta como se explica en los libros de la nueva teoría del todo, es la teoría física menos científica que me podía imaginar para representar la realidad.
La teoría del observador ignorante
Este ejemplo, junto al de las pelotas de la luz, es de los que más me gustan.
Esta discusión no es seria puesto que la Relatividad Especial está superada y matizada por la propia Relatividad General. Especialmente en este caso al establecer un sistema de referencia privilegiado. No obstante, forzará al lector a concentrarse y darse cuenta de lo fácil que es confundirse con tanta terminología inapropiada. El experimento de la Abrujuela sobre simultaneidad es muy parecido y complementario y se encuentra en el libro Experimentos de Física Global.
En los libros sobre la Relatividad Especial de Einstein suele estar repetido en varios ejemplos, pero todos ellos tienen la misma idea básica. Imaginemos un par de observadores inerciales para el momento t igual a 0, uno de ellos en el centro de un vagón de un tren que se mueve con una velocidad que no es ni grande ni pequeña. El otro observador inercial se encuentra parado en la estación a la misma altura que el anterior.
Justo en ese momento caen un par de rayos en los dos extremos del vagón. (Lo sabemos porque nosotros ponemos el ejemplo, si no fuese así sería difícil saberlo con certeza).
Experimentos de ciencia 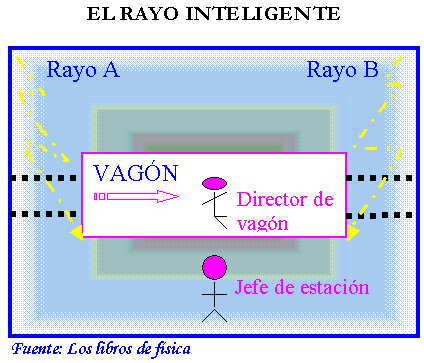
El observador inercial de la estación, digamos que es el jefe de estación, se encuentra en un sistema inercial fijo al andén. Este observador verá los dos rayos al mismo tiempo porque la distancia de donde cayeron a donde él se encuentra es la misma y como sabe que la velocidad de la luz es siempre la misma (lo había estudiado con antelación) deduce que los rayos son simultáneos.
A este observador inercial lo vamos a considerar inteligente y además sabemos que era jefe de algo.
El observador inercial que está en el vagón, director del vagón, se encuentra en un marco inercial solidario con el vagón. Como el vagón está en movimiento percibe primero el rayo que cayó en un sayo, perdón, digo en la parte delantera del vagón por el efecto de que se va acercando a dicha parte.
Al ver los dos rayos con un pequeño desfase temporal deduce (tenía ojos de plato como los búhos), por aquello de la velocidad constante de la luz (que también lo había estudiado) que los dos rayos no cayeron simultáneamente.
Conclusión de la Relatividad Especial ortodoxa de Einstein: dos sucesos que son simultáneos para un observador no lo son para otro observador inercial que se mueva respecto al primero
Mi conclusión: siguiendo el método científico y el sentido común, a este observador lo podemos considerar, como poco, ignorante. Podía haber tenido en cuenta el tiempo en recibir la información de la realidad y su desplazamiento durante dicho tiempo para hacerse una idea de la misma, es lo normal. ¿No? ¡Después de haberlo estudiado y todo!
¡Rayos y truenos! No quiero ni imaginar lo que habría pensado después de escuchar los truenos correspondientes porque la diferencia temporal entre los mismos sería mayor y le causaría contrariedades mentales con las diferentes simultaneidades bosquejadas.
Otra situación mental podría darse si caen dos rayos, pero uno de ellos le cae encima al observador ignorante; en este caso particular, como para este observador el tiempo se detiene indefinidamente pensaría que todos los posteriores rayos del universo serían simultáneos; y le podríamos denominar el observador iluminado.
El primer observador era tremendo, porque se dio cuenta que los rayos habían caído justo en las puntitas del vagón a pesar de que los vio, uno detrás del vagón y otro algo metido en la parte delantera (debía tener ojos de águila). Se rumorea que era mejor que el enanito rojo de Venus.
Como siempre, la neurona lista ya está levantando la dendrita para preguntar: ¿qué hubiera pasado si hubiésemos cambiado los observadores de sitio?
