2. JUEGO DE SIMULACIÓN DE LA EVOLUCIÓN CON ALGORITMOS GENÉTICOS
Al igual que las técnicas del billar, trucos y efectos incluidos en el juego de evolución son excelentes para entender el juego de fuerzas que se estudia en física, el juego de evolución Esnuka también es muy útil para entender la técnica de la evolución entendida según la Teoría General de la Evolución Condicionada de la Vida (ECV) y las leyes de Mendel.
La opción de simulación del menú del juego de evolución Esnuka nos permite observar el cambio producido en el potencial genético de la población para cada generación al jugar al billar; siendo ésta de 20, 30 ó 100 individuos, si el sonido está desactivado será 100.
Llamaré algoritmos genéticos a las reglas técnicas que determinan la evolución de los colores de las bolas que, en definitiva, representan los estados evolutivos de las mismas. Sin embargo, dudo mucho que la naturaleza utilice las matemáticas abstractas en su evolución. Conviene, pues, tener presente que los algoritmos genéticos son instrumentos de representación de las técnicas de la evolución según la ECV y adaptados para una mesa de billar.
El parámetro de nivel determina la forma de calcular en la simulación de la evolución los valores correspondientes al potencial inicial de los genes. Para valores 1 y 2 los valores de cada gen son aleatorios e independientes entre sí, por el contrario para valores 3 y 4 son aleatorios pero los genes de cada individuo tienen el mismo potencial inicial. Esta característica no afecta apenas a la simulación de la evolución, si bien en el segundo supuesto los valores tenderán a ser menos extremos por calcularse de dos en dos.
Esta opción se muestra en la pantalla con dos círculos diferentes o iguales respectivamente. No obstante lo anterior, si la función de inversión de colores está activada todos los genes se iniciarán con idéntico valor y se representará con un único círculo en la pantalla.
El citado parámetro de nivel de dificultad también determina la simulación de la evolución de acuerdo con las reglas del juego Esnuka - I para valores 1 y 3 ó Esnuka - II para valores 2 y 4; representándose con una o dos barras verticales en la pantalla.
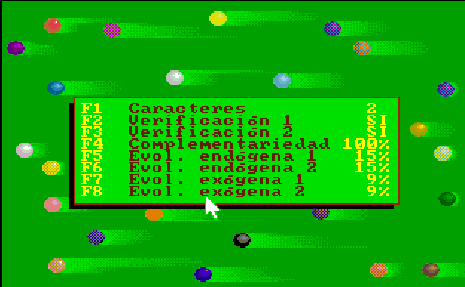
En todo caso, cuando se elige la opción del modelo de simulación, se usan las técnicas del programa de jugar al billar para calcular aleatoriamente el potencial inicial de cada gen de cada bola dentro de los límites de 1 a 3, en consecuencia, el color de las bolas dependerá de la configuración de los parámetros de verificación y complementariedad fijados y siempre corresponderá a la parte izquierda de la ventana de evolución.
Cada vez que se pulse una tecla, una nueva generación será calculada de acuerdo con los parámetros de evolución y, por supuesto, de los de verificación y complementariedad fijados en el menú de configuración y mostrados en la pantalla del programa.
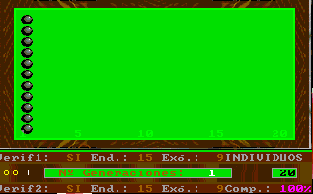
El detalle de cada proceso evolutivo individual es idéntico al utilizado para los juegos de villar Esnuka - I y de Esnuka - II y las reglas técnicas que rigen el intercambio de los genes son las clásicas de Mendel con probabilidades de transmisión iguales para cada uno de los genes.
De esta forma se consigue observar el efecto sobre la evolución que tienen los conceptos de Verificación Lógica de la Información y de caracteres complementarios.
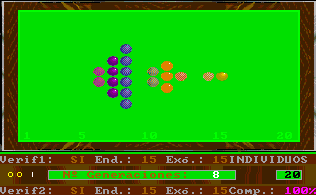
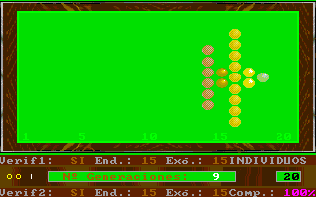
En particular, la existencia de verificación externa hace que las figuras se asemejen a una punta de flecha; si además se da la complementariedad, se deforma la figura anterior, recordándonos, en ocasiones, a los fractales.
La velocidad de la evolución depende de los parámetros de la evolución y es la misma con o sin verificación externa; ahora bien en el primer supuesto se producirá un desfase temporal respecto al segundo.
Otro efecto reconocible en la simulación de la evolución es el distanciamiento de los individuos de la población cuando los parámetros de evolución endógena son pequeños con relación a los de evolución exógena y viceversa.
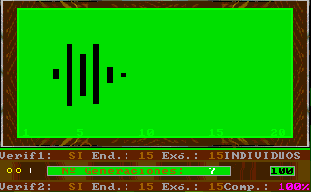
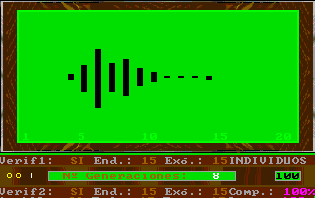
Para estudiar el comportamiento de la evolución a largo plazo, se pueden fijar los parámetros de evolución endógena y exógena muy pequeños, esto es equivalente a no cambiar los parámetros y aumentar las dimensiones de la ventana de la evolución y por consiguiente la distancia entre dos colores.
Las diferencias entre colores consecutivos son siempre constantes y los parámetros de evolución endógena y exógena están expresados en porcentajes.
Como explicación técnica adicional, señalar que los colores siempre están normalizados en la escala 1 a 20. El potencial representado por los colores coincide en el caso de genes, caracteres e individuos excepto para el caso de individuos con dos caracteres complementarios. Por ejemplo, el potencial resultante de dos caracteres complementarios puede ser, de acuerdo con la teoría explicada, el producto de sus potenciales respectivos para el caso de complementariedad perfecta, siendo necesaria para su representación su normalización; es decir, si el potencial de los dos caracteres fuese de 10 el potencial del individuo será 10 * 10 = 100, para normalizar el rango de 1 - 400 a 1 - 20 tenemos que dividir por 20 y por lo tanto la bola aparecer con valor 100 / 20 = 5 ( columna 5)
