2. JEU DE SIMULATION DE L'EVOLUTION AVEC DES ALGORYTHMES GENETIQUES
De même que les techniques du billard, les trucs et les effets inclus ans le jeu d'évolution sont excellents pour comprendre le jeu de forces qui s'étudie en physique, le jeu d'évolution Esnuka est également très utile pour comprendre la technique de l'évolution comprise d'après la Théorie Générale de l'Evolution Conditionnelle de la Vie (ECV) et les lois de Mendel.
L'option de simulation du menu du jeu d'évolution Esnuka nous permet d'observer le changement survenu dans le potentiel génétique de la population pour chaque génération en jouant au billard ; cette option est de 20, 30 ou de 100 individus ; si le son est désactivé, il est de 100.
J'appellerai algorithmes génétiques les règles techniques qui déterminent l'évolution des couleurs des boules qui, en définitive, représentent les états évolutifs de celles-ci. Néanmoins, je doute fortement que la nature utilise les mathématiques abstraites dans leur évolution. Il convient par conséquent d'avoir en tête le fait que les algorithmes génétiques sont des instruments de représentation des techniques de l'évolution selon la ECV et adaptés à une table de billard.
Le paramètre de niveau détermine la façon de calculer dans la simulation de l'évolution les valeurs qui correspondent au potentiel initial des gènes. Pour la valeur 1 et 2, les valeurs de chaque gène sont aléatoires et indépendantes entre elles ; au contraire, pour les valeurs 3 et 4, elles sont aléatoires mais les gènes de chaque individu ont le même potentiel initial. Cette caractéristique n'affecte presque pas la simulation de l'évolution, par contre, dans la seconde hypothèse, les valeurs auront tendance à être moins extrêmes car elles se calculent de deux en deux.
Cette option apparaît sur l'écran avec deux cercles différents ou égaux respectivement. Malgré ce qui a été mentionné antérieurement, si la fonction d'inversion des couleurs est activée, tous les gènes seront initiés avec une valeur identique et représentés avec un cercle unique sur l'écran.
Le paramètre de niveau de difficulté mentionné détermine également la simulation de l'évolution en accord avec les règles du jeu Esnuka – I pour les valeurs 1 et 3 ou Esnuka-II pour les valeurs 2 et 4 , avec une représentation sous forme d'une ou de deux barres verticales sur l'écran.
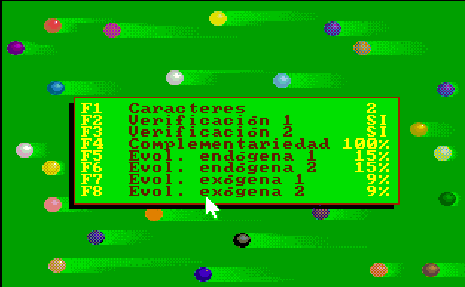
Dans tous les cas, quand on choisit l'option de modèle de simulation, on utilisera les techniques du programme pour jouer au billard pour calculer de façon aléatoire le potentiel initial de chaque gène de chaque boule dans les limites de 1 à 3, par conséquent, la couleur des boules dépendra de la configuration des paramètres de vérification et de complémentarité fixés et correspondent toujours à la partie gauche de la fenêtre d'évolution.
Chaque fois que l'on actionne une touche, une nouvelle génération est calculée, en accord avec les paramètres d'évolution et, bien sûr, les paramètres de vérification et de complémentarité fixés dans le menu de configuration et montré sur l'écran du programme.
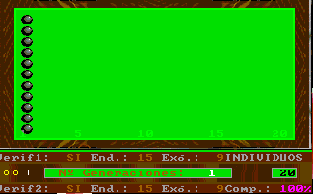
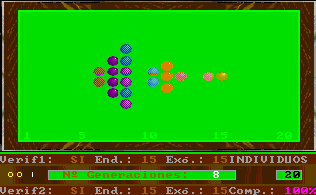
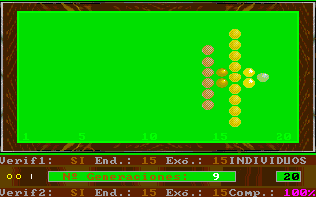
En particulier, l'existence de la vérification externe fait que les figures ressemblent à la pointe d'une flèche ; si, de plus, on a la complémentarité, la figure antérieure se déforme et nous rappelle ainsi, à certaines occasions, les fractales.
La rapidité de l'évolution dépend des paramètres de l'évolution et est la même avec ou sans vérification externe ; ceci dit, dans la première hypothèse se produira un déphasement temporel par rapport à la deuxième.
Un autre effet reconnaissable dans la simulation de l'évolution est la distanciation des individus de la population quand les paramètres d'évolution endogène sont petis par rapport à ceux de l'évolution exogène et vice-versa.
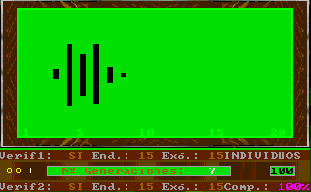
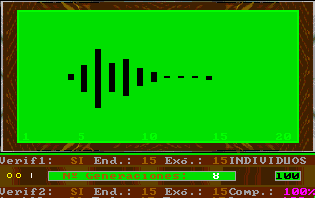
Pour étudier le comportement de l'évolution à long terme, on peut fixer les paramètres d'évolution endogène et exogène très petits, c'est la même chose que de ne pas changer les paramètres et augmenter les dimensions de la fenêtre de l'évolution et, par conséquent, la distance entre deux couleurs.
Les différences entre couleurs consécutives sont toujours constantes et les paramètres d'évolution endogène et exogène sont exprimés en pourcentages.
Comme explication technique supplémentaire, il faut signaler que les couleurs sont toujours normalisées dans l'échelle qui va de 1 à 20. Le potentiel représenté par les couleurs coïncide dans le cas de gènes, de caractères et d'individus, sauf en ce qui concerne le cas d'individus avec deux caractères complémentaires. Par exemple, le potentiel qui résulte de deux caractères complémentaires peut être, en accord avec la théorie expliquée, le produit de ses potentiels respectifs pour le cas d'une complémentarité parfaite, sa normalisation étant nécessaire à sa représentation ; c'est-à-dire, si le potentiel de l'individu est 10* 10=100, pour normaliser le rang de 1 - 400 à 1 – 20, nous devons diviser par 20 et par conséquent la boule va apparaître avec une valeur de 100 / 20 = 5 ( colonne 5)
