4.b.2. Courbure de la lumière de l'effet des lentilles gravitationnelles
La prédiction du comportement des étoiles comme des lentilles gravitationnelles sur la courbure de la lumière est la première des trois fameuses prédictions de la Relativité Générale d’Einstein et elle fut célèbre pour le retard dans sa confirmation expérimentale jusqu’à l’éclipse solaire de 1919.
Ce qui a aussi contribué à la célébrité de cette prédiction, c’est qu’elle suppose un effet de loupe gravitationnelle simple à visualiser et que la courbure de la lumière prédite et vérifiée par l’effet de lentille gravitationnelle était juste le double de celle qui résulterait de l’application de la Loi de la Gravité Universelle de Newton.
Il semble curieux que le continuum espace-temps s’étire-dilate dans la courbure de la lumière par effet de lentilles gravitationnelle avec un facteur *2* par rapport à ce qui est prévu par la Loi de Gravité de Newton et personne ne semble capable d’en donner la raison scientifique, et surtout expliquer pourquoi le chiffre est rond et si simple. Bien sûr, on recourt systématiquement aux équations de champ d’Einstein, mais rien d’autre.
En cherchant sur Internet –voir l’article bending Light en mathpages.com– ou en demandant à n’importe quel ami qui ait une réelle connaissance des mathématiques et de la géométrie elliptique, celui-ci vous dira qu’une particule qui passe près du Soleil décrit une hyperbole vu qu’il se comporte comme une lentille gravitationnelle. En plus, que en fonction de son excentricité, pour des valeurs très petites de m par rapport à r0 et selon la Loi de Gravité de Newton, l'angle ou courbure totale de la lumière serait égal à :
α = 2 m /r0 = 0,875'' d'arc
Où m est la masse du Soleil en unités géométrie –la masse multipliée par G ou constante de gravitation et divisée par la vitesse de la lumière au carré– et r0 la distance la plus proche du rayon de lumière au Soleil.
Rappelons quelques bases de géométrie du cercle, un tour entier fait 360° degrés, chaque degré fait 60’ minutes et chaque minute 60’’ seconde d’arc.
Par conséquent, l’angle ou courbure de la lumière qui provoquerait les lentilles gravitationnelles dans la Loi de la Gravitation Universelle de Newton est directement proportionnel à la masse qui crée le champ de gravité, comme la force centripète est directement proportionnelle à la masse.
Même si une planète a une masse, pour la Mécanique Classique, on ne prend pas en compte cette masse, vu que une force gravitationnelle s’exerce sur la planète en fonction de sa masse gravitationnelle, mais la force par unité de masse gravitationnelle reste constante y compris si on prenait en compte la masse cinétique d’après la Théorie de la Relativité d’Einstein –masse équivalente à l’énergie cinétique.
Et donc, accord avec la Loi de la Gravité Globale il y a une force supplémentaire, la seconde composante de l’atractis causa ou effet Merlin est due à la vitesse et opère sur la masse cinétique. La masse globale est la masse au repos plus la masse équivalente à l’énergie cinétique. Dans le cas de la masse reste la lumière n'existe pas.
Dans la partie de la Loi de la Gravité Globale de ce livre, on a commenté que cette loi devrait être exprimée en terme d’énergie et non de masse, vu que l’interaction gravitationnelle se produit par un transfert entre l’énergie du champ de gravité et l’énergie élastique sous forme de masse, masse cinétique ou directement sous forme d’énergie électromagnétique.
Pour calculer la courbure de la lumière sous l’effet des lentilles gravitationnelles sur l’énergie électromagnétique, il ne nous reste qu’à vérifier que la seconde composante ou force de gravité additionnelle dérivée de la vitesse, soit égale quantitativement à la force de gravité de la première composante.
Le cas de l’énergie électromagnétique est simplement intuitif, vu que la valeur de l’énergie cinétique de la lumière sera égale à l’énergie cinétique équivalente à la supposée masse équivalente.
Anneau Einstein (NASA) (Image du domaine public)

D’un autre point de vue, si la première composante de l’atractis causa est due à la vitesse de propagation de la tension longitudinale d’Ether Global et est égale à la vitesse de la lumière, et la seconde composante –effet Merlin– est due à la vitesse de la lumière dans le cas de l’énergie électromagnétique. En conséquente, les deux composante de l’atractis causa devraient avoir la même valeur et la courbure de la lumière par les lentilles gravitationnelles sera le double de celle que nous obtiendrions avec la Loi de Gravitation de Newton.
L’explication précédente de la cause physique de l’effet des lentilles gravitationnelles ou courbure de la lumière est un résumé de ce qui est commenté dans la deuxième partie de ce livre, et dans les parties sur le mouvement avec symétrie totale et symétrie radiale de la gravité dans le livre Physique et Dynamique Globale.
Cependant, pour les amateurs de mathématiques, on a rajouté l’analyse quantitative suivante, qui en plus de posséder une certaine valeur éducative, est, en quelque sorte commune à la Physique Globale et à la Théorie de la Relativité.
ANALYSE QUANTITATIVE
J’ai déjà commenté que l’incrément de masse avec la vitesse est un aspect partiellement correct de la Théorie de la Relativité –si on introduit le système de référence naturel pour la vitesse physique–, et, par conséquence, ce concept reste dans la Physique Globale, sur la base, dans ce dernier modèle, de l’observation expérimentale pure et sur les mécanismes de transfert énergétique de l’interaction gravitationnelle, à l’opposé de l’imposition des axiomes mathématiques à la Physique.
Dit de cette manière, il n’ait pas nécessaire de maintenir la Théorie de la Relativité pour accepter l’incrément de masse physique cité avec la vitesse.
La fameuse formule de la masse globale qui sert à déduire l’énergie cinétique en terme relativiste est la suivante :
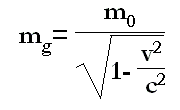
masse globale = masse au repo + masse cinétique
[2.a] m = m0 /(1 - v²/c²)½
Ou pour faire court,
m = γ m0
Comme indiqué dans la Théorie de la Relativité d'Einstein, l'énergie cinétique est équivalente à l'augmentation de la masse au repos m0
Le développement en série du théorème de Taylor de la constante γ nous donne :
γ = 1+½ v²/c² +3/8 v4/c4+5/16 v6/c6+...
Energie cinétique = m0 [ ½ v²/c² +3/8 v4/c4+5/16 v6/c6+...]
Avec ces effets, la remarquable équation de la masse globale ne doit pas contenir la simplification réalisée pour l'énergie cinétique classique dans le développement en série du théorème de Taylor, vu que le second terme de la parenthèse devient significatif pour des vitesses de l'ordre de celle de la lumière.
Comme un bon Einsautre, j’ai demandé à un ami mensiste, qui faisait des sciences exactes à l'université, et il m’a répondu qu’il en avait assez de calculer des dérivées de troisième ordre, et bien sûr je le comprends et nous sommes toujours amis.
En marge de ces anecdotes sympathiques, au niveau du développement en série du théorème de Taylor, les seuls termes valides sont ceux qui correspondent aux dérivés de la fonction, si et seulement si ces dérivées existent, c’est-à-dire, différentes de zéro. En général, mathématiquement, dans l'équation précédente, on calcule le dernier terme valide de manière à ce qu’il reprenne les termes éliminés.
Dans notre cas, si on additionne (1/8 v4/c4) au second terme, on reprend l'effet résiduel du reste des termes éliminés et il nous restera :
Energie cinétique = m0 [½v²/c²+½v4/c4]
Logiquement, le premier terme de la parenthèse n’est pas significatif pour des vitesses faibles, non planétaires, alors que le second terme peut être négligé pour les vitesses planétaires mais pas par les vitesses de l’ordre de celle de la lumière et encore moins pour la vitesse semblable au cas de l’effet des lentilles gravitationnelles. Par conséquent, dans une analyse générale, il faut prendre en compte toutes les possibilités de valeur de la vitesse de la masse physique pour déterminer la force de gravité totale.
Et dans le même sens, dans l'équation (2) de la page en anglais de Mathpages.com ** sur l'inertie de l'énergie, il y a une utilisation du même développement en série du théorème de Taylor.
La démonstration de la Relativité Générale du fait que l’effet des lentilles gravitationnelles est le double par rapport à la Loi de Gravitation de Newton est assez compliquée, mais il semble qu’inévitablement, le même développement en série de Taylor soit utilisé, comme on peut le voir sur la page de la Courbure de la lumière du site Mathpages.com cité plus haut.
Au contraire, sans parler du développement en série de Taylor, dans la Physique Globale, le calcul ne peut pas être plus simple.
Ensuite, l’angle de la courbure de la lumière par effet de lentilles gravitationnelle sera le double de celui que prédit la Loi de la Gravitation Universelle de la théorie de Newton, comme on le savait déjà avec les célèbres observations de l’éclipse de Soleil de 1919 et les suivantes la valeur étant 1,75’’ d’arc.

