4.b.3. Relativité d’Einstein et orbite de la planète Mercure
Si la prédiction de la Théorie de la Relativité Générale d’Einstein sur la courbure de la lumière est la plus remarquable et spectaculaire, par son mode de vérification avec l’observation de l’éclipse de 1919, l’explication de la précession du périhélie de Mercure –déviation par rapport à la Mécanique Céleste de Newton– est la plus effective par son aspect quantitatif.
Cependant, il convient de noter que, en 1898, Paul Gerber a expliqué cette précession avant la physique relativiste avec exactement la même formule.

Les astronomes avaient observés une déviation par rapport à la Mécanique Céleste de Newton qui n’était expliquée par aucun facteur connu, déviation de 43,11’’ d’arc en 100 ans sur l’axe de l’orbite de la planète Mercure. Cette déviation de l’orbite est celle à laquelle je vais me référer avec précession du périhélie de Mercure, précession de l’orbite de Mercure ou précession de Mercure, bien qu’au sens strict, la précession totale ou somme des précessions expliquées ou non soit relativement supérieure. Si on calcule en grade, à l’année, la précession non expliquée, on obtient en chiffre rond un dix-millième de degré par an.
Par les extraordinairement compliquées équations de champ de la Mécanique Relativiste, Einstein arrive à un chiffre très proche de 43’’ secondes d’arc de précession de l’orbite de Mercure. –Voir le site de mathpages ** sur l’explication de la Relativité Générale de la précession anormale de l’orbite de Mercure.
Il n’est pas étonnant que face à cet arrangement des orbites des planètes obtenu par la Théorie de la Relativité Générale, on ait fini par accepter la relativité dans son ensemble, en discréditant d’autres alternatives moins aventureuses. Il est indiscutable que les équations de la Relativité Générale d’Einstein contiennent quelques règles valides de comportement de la nature bien qu’elles soient embourbées dans ses mécanismes de procédures et de calculs, comme les idées de Paul Gerber.
Voyons maintenant si les Lois de la Gravité Globale expliquent elles aussi la précession du périhélie de Mercure.
L’expression de l’accélération de la gravité de la formule apportée par la Loi de la Gravité Globale nous donne directement les résultats recherchés sur la déviation angulaire et la composante normale de l’accélération ou accélération centripète.
Pour connaitre la déviation angulaire totale en un tour ou orbite de mercure, la seule chose qu’il faut faire, c’est de substituer les variables par leurs valeurs, en tenant compte de l’accélération gg qui devra représenter l’accélération centripète autant due à la force de gravité correspondant à la loi de Newton qu’à à l’effet Merlin ou seconde composante de l’atractis causa ajoutée par les Lois de la Gravité Globale.
C’st-à-dire que gg sera la composante normale de l’accélération ou accélération centripète provoquée par un tour complet de l’orbite de la planète plus la précession observée pour la période T.
Cette période T, par définition de sa valeur en trigonométrie, occasionnera un tour complet exactement si on considère exclusivement la Loi de la Gravitation Universelle de Newton, vu que nous savons qu’une ellipse parfaite serait une conséquence de la loi de l’inverse du carré du rayon, comme on l’observe dans les lois de Kepler déduites des orbites des planètes de la Mécanique Céleste.
Don Magufo m’a montré comment calculer rapidement la composante normale de l’accélération grâce à un petit cours de mathématiques intuitives. Mais avant de continuer, je vais rappeler les données nécessaires pour effectuer les calculs, et en plus de l’inutile v :
G = constante de gravitation universelle = 6,67266 * 10-11 (m² N / kg²)
c = vitesse de la lumière = 2,99792458 * 108 (m/s)
M = masse du Soleil = 1,98892 * 1030 (Kg.)
r = rayon moyen de l'orbite de Mercure = 57,9 * 106 (m)
T = période orbite de Mercure = 7,60018 * 106 secondes = 414,9378 orbites en 100 ans.
v = vitesse moyenne de Mercure = 47948,31 (m/s)
Pour vérifier empirement la formule de dynamique de la planète Mercure comme pour une partie de la Mécanique Céleste des planètes et astres, on a suivi les étapes suivantes :
Simplification au cas d'une orbite planétaire circulaire.
On a considéré le cas d’une orbite circulaire de la planète pour simplifier les calculs, parce que le jeu de force de la gravité continuera d’exister et l’excentricité de l’orbite de la planète Mercure est assez basse. Bien sûr, c’est suffisant pour ma proposition ici.
Calcul des tours par période avec la Loi de Gravité de Newton.
La formule de la Loi de la Gravité Global peut être écrite avec ses deux composantes :
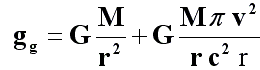
Où le premier terme de la partie droite est la gravité de la loi de Newton ou accélération centripète. La variation angulaire produite par cette dernière devrait normalement être, égale à un tour ou 2π radians.
Donc, si on le multiplie ou on le divise par v² et qu’on substitue v²/r par la composante normale de l'accélération ou accélération centripète an, il nous restera :
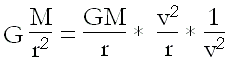
t en rappelant que la valeur de la vitesse orbitale est la racine carrée de GM/r, nous aurons :
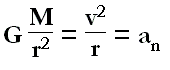
v T = 2πr
w T = 2π
v / r = w
an / v = w
an T / v = T (v²/r) (1/v)
= Tv/r = wT =
= 2π Radians Q.E.D.
Comme la composante normale de l'accélération an est en relation avec le changement de direction de la vitesse en fonction du temps, si on calcule ce changement pour chaque m/s (en la divisant par v) et qu’on la multiplie par la période T ou nombre de secondes totales en un tour, on obtiendra, par trigonométrie 2π radians ou un tour complet de l'orbite de la planète Mercure ou n’importe quelle autre planète ou astre de la Mécanique Céleste.
Analytiquement le raisonnement serait :
Le raisonnement précédent peut être vérifié en utilisant la valeur de la vitesse moyenne de la planète Mercure –un tour entier a 2π radians ou 360° degrés, chaque degré fait 60’ minutes et chaque minute 60’’ secondes d’arc.
Accélération centripète
et vitesse linéaire de la planète MercureG 6,67266E-11 Masse du Soleil 1,98892E+30 GM 1,32714E+20 Rayon moyenne orbite 5,79000E+10 an= GM/r² 3,95876E-02 v moyenne Mercure 4,794831E+4 an / v = w 8,25631E-07 Tours en 100 ans 4,149378E+02 Période T de l'orbite 7,60018E+06 w * T = 2 π 6,27494E+00 Calcul des tours par période dus à l'effet Merlin.
Ce qui nous intéresse vraiment, c’est la seconde composante de la formule de la Loi de la Gravité Globale ; vu que ce sera l’accélération centripète provoquée par effet Merlin, ou si on préfère, par l’énergie cinétique. Cette accélération centripète occasionnera la précession du périhélie de Mercure (ppm), ou de l’orbite de n’importe quelle planète de la Mécanique Céleste, si on la calcule pour toute la période considérée comme on l’a fait précédemment avec a(n) pour calculer les 2π radians.
Selon Don Magufo, on peut résoudre directement l'intégrale intuitive de l'équation différentielle non posée si, une fois substituée v²/r par a(n), on met sa valeur pour une période entière ; qui, comme nous venons de le voir plus sera 2π en terme de trigonométrie.
L'intégrale formelle par rapport à la période de temps de l'accélération centripète se résout sans aucun problème, car la vitesse que l'accélération centripète comme le reste des variables sont constantes et indépendantes du temps avec la simplification à une orbite circulaire de la planète Mercure. D'ailleurs, elle coïncide avec les calculs basiques de trigonométrie car l'intégrale de *dt* est 1.Ainsi, il restera :
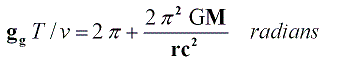
Et donc, la précession du périhélie de Mercure en radians sera :

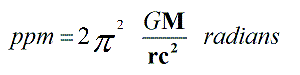
La valeur de la ppm obtenue avec l’égalité antérieure, dérivée de la Physique Globale et de 43,08’’ seconde d’arc tous les 100 ans, comme il est montré dans le tableau suivant :
Calcul de la précession du périhélie
de la planète MercureG 6,67266E-11 Masse du Soleil 1,98892E+30 GM 1,32714E+20 Rayon moyenne orbite 5,79000E+10 an= GM/r 2,29212E+09 c² 8,98755E+16 GM / r c² 2,55033E-08 π 3,141592654 π GM / r c² 8,01210E-08 2 π Radian/tour 6,283185307 ppm = 2π² GM / r c² 5,03415E-07 Tours en 100 ans 4,14938E+02 radians/100 years 2,08886E-04 Secondes/radian 2,06265E+05 Arc sec./100 ans 4,30858E+01 * * *
Rappelons que si dans cette formule, on changeait 2π pour 6, on obtiendrait la formule obtenue Paul Gerber 1898 et par Einstein dans la Relativité Générale indépendamment de l’excentricité, comme on le mentionne dans le livre de la Théorie de la Relativité, Eléments et Critique.
Pour la Terre, la Relativité Générale donne une valeur de 3,8 secondes d’arc, la Physique Globale de 4,02 et la valeur observée est de 5 secondes d’après la page Internet de Mathpages citée précédemment.
Bien qu’il n’y pas de doute pour que les deux théories soient deux approximations correctes – trois si l'on inclut Paul Gerber– ou formes de voir la même chose par rapport à l’orbite de Mercure, il faut faire ressortir que les deux sont incompatibles entre elles, car on expliquerait deux fois la même déviation angulaire.
| Rayon moyen 106 km |
Planètes | Radians | Tours en 100 ans |
Total radians | Précession (seconde d'arc) | ||
|---|---|---|---|---|---|---|---|
| Observé | RG | FG | |||||
| 57,90 | Mercury | 5,03415E-07 | 414,93780 | 2,08886E-04 | 43.10 | 42,9195 | 43,08581 |
| 108,20 | Vénus | 2,69387E-07 | 162,60160 | 4,38028E-05 | 8.65 | 8,6186 | 9,03498 |
| 149,60 | Tierra | 1,94838E-07 | 100,00000 | 1,94838E-05 | 3,85 | 3,8345 | 4,01882 |
| 227,90 | Mars | 1,27897E-07 | 53,19150 | 6,80303E-06 | 1,36 | 1,3502 | 1,40323 |
| 778,30 | Jupiter | 3,74505E-08 | 8,43170 | 3,15771E-07 | 0,0623 | 0,06513 | |
| 1427,00 | Saturno | 2,04259E-08 | 3,39440 | 6,93336E-08 | 0,0137 | 0,01430 | |
| 2869,60 | Urano | 1,01574E-08 | 1,19030 | 1,20904E-08 | 0,0024 | 0,00249 | |
| 4496,60 | Neptune | 6,48217E-09 | 0,60680 | 3,93338E-09 | 0,0008 | 0,00081 | |
| 5900,00 | Pluton | 4,94029E-09 | 0,40320 | 1,99193E-09 | 0,0004 | 0,00041 | |
En plus elles se basent sur des principes différents et contradictoires, ce que rendrait inutile de recourir au rasoir d’Occam, car il existe d’autres phénomènes naturels ou expérimentaux de physique qui aideraient à faire pencher la balance définitivement.
Avec les Lois de la Gravité Globale, nous avons vérifié qu’on expliquait exactement la précession du périhélie de Mercure, comme une conséquence de l’effet Merlin au niveau de l’interaction d’Ether Global avec les corps avec masse.
En d’autres termes, le principe de l’égalité entre masse gravitationnelle et masse inertielle établie par Newton et conservé par Einstein est vague et inutile, pars que le comportement de la masse physique dans son interaction avec l’Ether Global est le même qu’elle soit étudiée avec ou sans le champ de gravitation, bien que les forces qui agissent sont différents.
Dans la partie sur la Deuxième Loi de Newton ou Loi de la Force du livre Physique et Dynamique Globale, on détaille les différences entre la conception de Newton, d’Einstein et de la Physique Globale elle-même, à cause des changements intrinsèques au sien de la masse et des forces agissant.
D'autres expériences liées aux orbites planétaires se trouvent aux pages sur le Gravity Probe-B de ce livre et le Paradoxe du Dernière Dauphin de livre Astrophysique et Cosmologie Globale.
Finalement, je voudrais remarquer qu’à aucun moment on a abandonné la géométrie non courbe de l’espace euclidien, malgré l’orbite de la planète Mercure, et bien que a Physique Globale soit supportée par un modèle physique consistent avec un temps absolu.
Quand Einsautre eut terminé la page Web,
il s’en alla le cœur léger le conter à Princoq
et celui-ci de répondre:
–Très bien. Et qu’as-tu fait ensuite?–
Einsautre, hésitant un peu, lui dit :
–Je me suis mis à joué avec mes billes
et à penser au numéro π.
Alors apparu une petite bourge,
qui se jeta à mes pied,
et ouvrit ses pijambes…
regardant fixement mes piboules.–
Et Princoq commenta :
–Quel pipompeux!–